-
![]() Picture: MFM/Peter Stein
Picture: MFM/Peter SteinConversion of STXM-derived intensity maps into detailed chemical composition maps for V2O5 nanowire electrodes. -
![]() Picture: MFM/Ying Zhao
Picture: MFM/Ying ZhaoModeling of inter-particle phase separation phenomena. The left-hand and middle images show simulated and experimentally observed domain structures of high/low Li concentration in V2O5 nanowire electrodes, respectively. The right-hand image shows simulated domain structures in electrode particle agglomerates. -
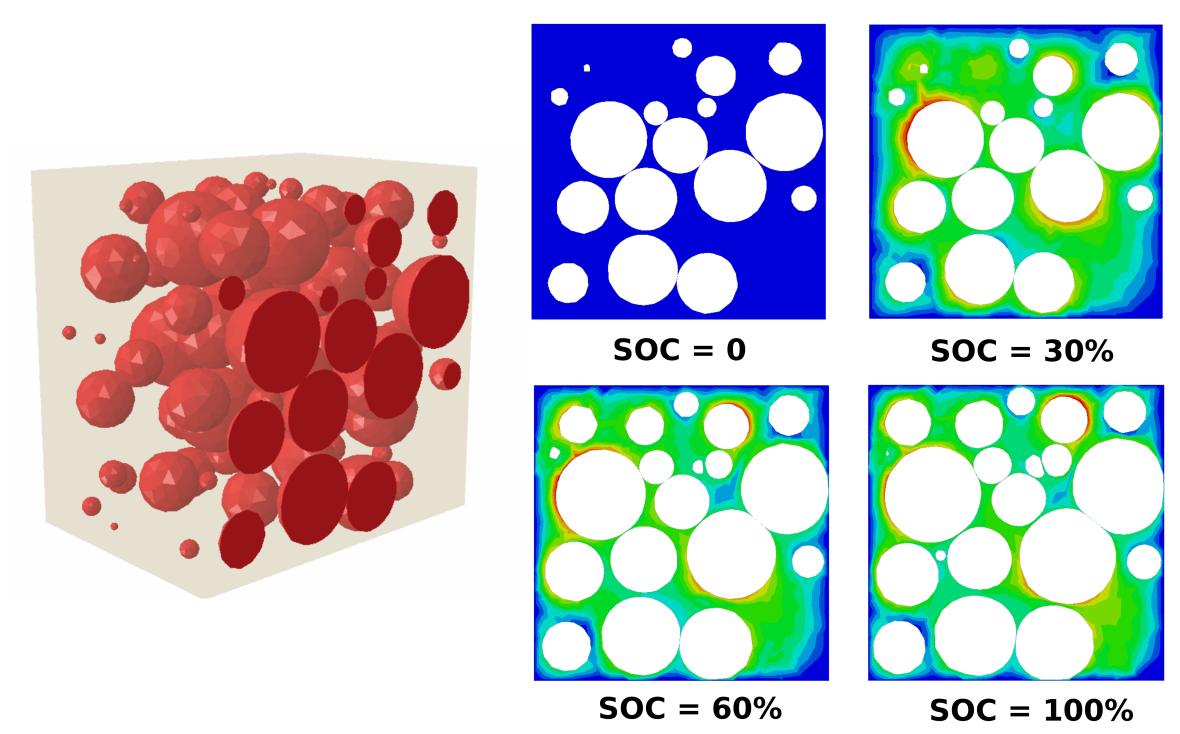
![]() Picture: MFM/Mamun Al-Siraj
Picture: MFM/Mamun Al-SirajDeformation of the electrochemically active polymer matrix in a composite electrode for an all-solid-state battery cell. The active storage particles (shown in red on the left-hand side) are rendered as white pores in the right-hand image. -
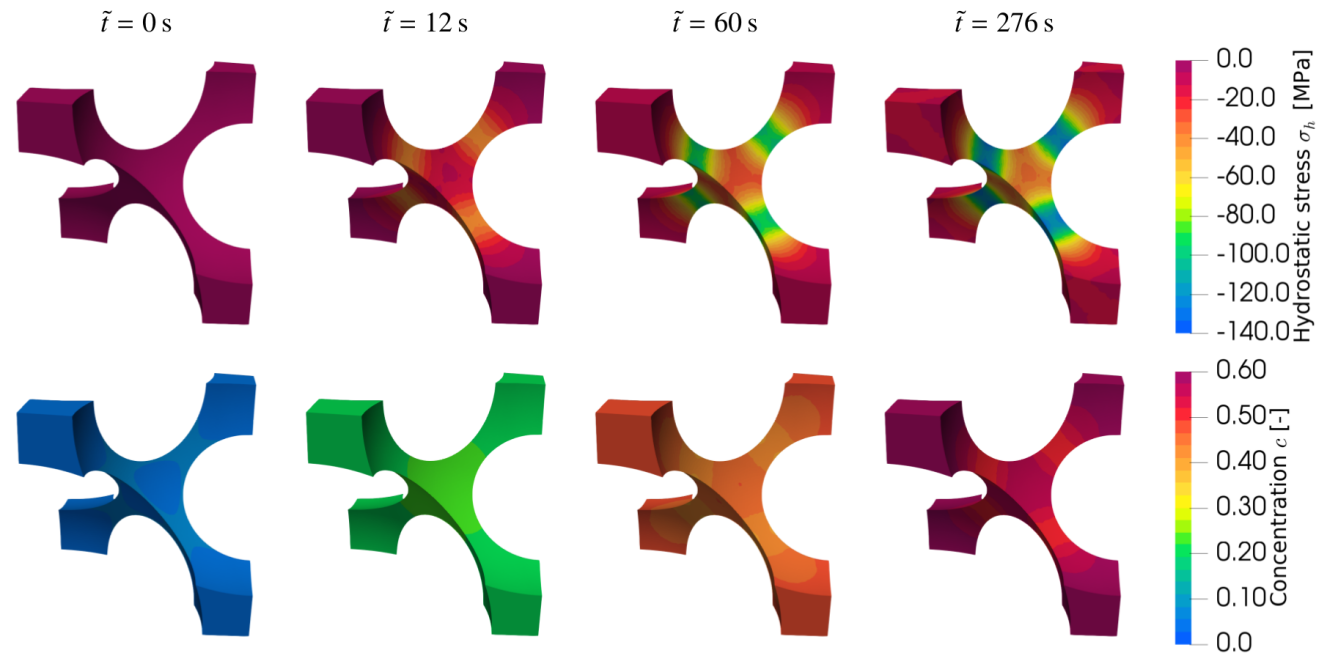
![]() Picture: MFM/Peter Stein
Picture: MFM/Peter SteinTemporal evolution of the concentration and hydrostatic stress field in a unit cell of an inverse-opal-structured battery electrode with a pore radius of 250nm. -
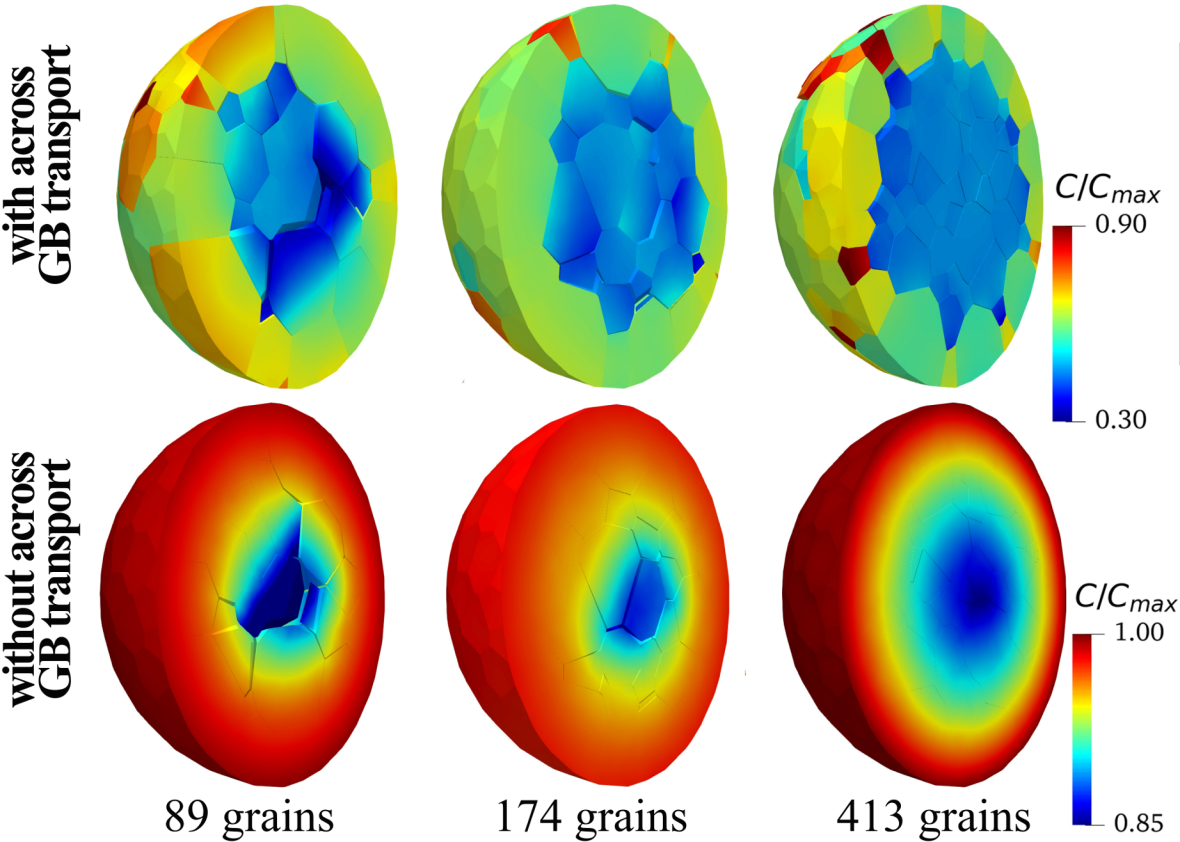
![]() Picture: MFM/Yang Bai
Picture: MFM/Yang BaiComparison of the concentration distribution in NMC electrode particles under across-grain ion transport.
- Go to picture 1
- Go to picture 2
- Go to picture 3
- Go to picture 4
- Go to picture 5
Objectives
With our research, we pursue the following objectives
- gain a mechanistic understanding of the damage initiation and growth, stress-assisted ionic transport, and stress-modulated surface reactions,
- predict the behavior of the storage material's behavior and of battery cells under cyclic operation and thus their performance and life span, and
- develop strategies for the optimization of electrode/electrolyte materials and of cell designs.
Methods
- Finite Elements (isoparametric, isogeometric, finite cell)
- Electrochemical modeling, phase-field methods
- Multiscale modeling
Current topics
Nanostructured electrodes have gained wide attention in the battery community since they exhibit a higher robustness against degradation. This can be attributed to surface effects that, while being negligible at macroscopic length scales, make contributions to a material's properties at atomistic length scales, leading, for instance, to size-dependent elastic properties.
In this project, we investigate the impact of surface stresses on the mechanical and the electrochemical behavior of nanostructured battery electrodes.
Solid-state batteries possess a distinct avantage over batteries with liquid electrolytes: they are much safer due to the absence of flammable electrolyte. This advantage however, comes at the price of a higher sensitivity against mechanical effects. For that reason, we investigate in this project the impact of mechanical deformation and stresses on the transport properties of composite electrodes for solid-state batteries.
A promising building block for battery electrodes are hierarchical “meatball” electrode particles. A large “secondary” particle is thereby comprised of several smaller “primary” particles, whose adhesion is primarily driven by van der Waals forces. This project is thus concerned with modeling crack formation and propagation in these particle agglomerates,
The diffusion of ions and phase separation phenomena within electrode materials in Lithium-ion batteries (LIB) can induce mechanical stress, which is known to be one of the main mechanism for the battery performance degradation. This highlights the importance of precise modeling of electro-chemo-mechanical performance for the battery cell. In this project, a two-level finite element framework is proposed to predict the LIB cell performance, which extends the common pseudo-2D (P2D) cell model and incorporates a mechanically coupled phase-field Cahn-Hilliard diffusion model of active particles. It is not only numerically more efficient than the rigorous microstructure-based battery cell models, but also inherits the full advantages of the particle models, i.e. the accuracy of the diffusion solution and accessibility to the complex particle geometry and defects in particles.
Dynamic modeling of all-solid-state batteries (SSBs) has gained strong research interest in recent years. However, the intrinsic equilibrium state, important for the exchange current calculation and the interface resistance analysis is hardly addressed. In this work, we investigate the intrinsic equilibrium state which takes the space charge layer and the unoccupied regular lattice sites (vacancies) into consideration. Moreover, the high interface impedance of the space charge layer and the polarization effect are still confusing and under discussion. Thus, we hope to introduce a more physical equivalent circuit model to explain such phenomena in the space charge layer.