A mixed formulation for physics-informed neural networks as a potential solver for engineering problems in heterogeneous domains: comparison with finite element method

Authors: Shahed Rezaei, Ali Harandi, Ahmad Moeineddin, Bai-Xiang Xu, Stefanie Reese

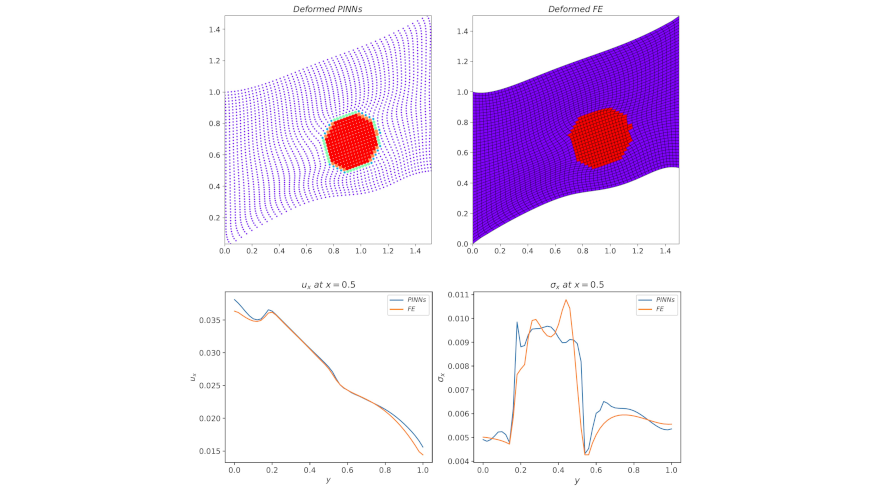
Physics informed neural networks (PINNs) are capable of finding the solution for a given boundary value problem. Here, the training of the network is equivalent to the minimization of a loss function that includes the governing (partial differential) equations (PDE) as well as initial and boundary conditions. We employ several ideas from the finite element method (FEM) to enhance the performance of existing PINNs in engineering problems. The main contribution of the current work is to promote using the spatial gradient of the primary variable as an output from separated neural networks. Later on, the strong form (given governing equation) which has a higher order of derivatives is applied to the spatial gradients of the primary variable as the physical constraint. In addition, the so-called energy form of the problem (which can be obtained from the weak form) is applied to the primary variable as an additional constraint for training. The proposed approach only required up to first-order derivatives to construct the physical loss functions. We discuss why this point is beneficial through various comparisons between different models. The mixed formulation-based PINNs and FE methods share some similarities. While the former minimizes the PDE and its energy form at given collocation points utilizing a complex nonlinear interpolation through a neural network, the latter does the same at element nodes with the help of shape functions. We focus on heterogeneous solids and check the performance of the proposed PINN model against the solution from FEM on two prototype problems: elasticity and the Poisson equation (steady-state diffusion problem). It is concluded that by properly designing the network architecture in PINN, the deep learning model has the potential to solve the unknowns in a heterogeneous domain without any available initial data from other sources. Finally, discussions are provided on the combination of PINN and data from physical FE simulations for a fast and accurate design of composite materials in future developments.