Phase-field simulation of misfit dislocations in two-phase electrode particles: Driving force calculation and stability analysis
New Publication in “International Journal of Solids and Structures”
2022/05/14
Authors: Xiandong Zhou, Christoph Reimuth, Bai-XiangXu
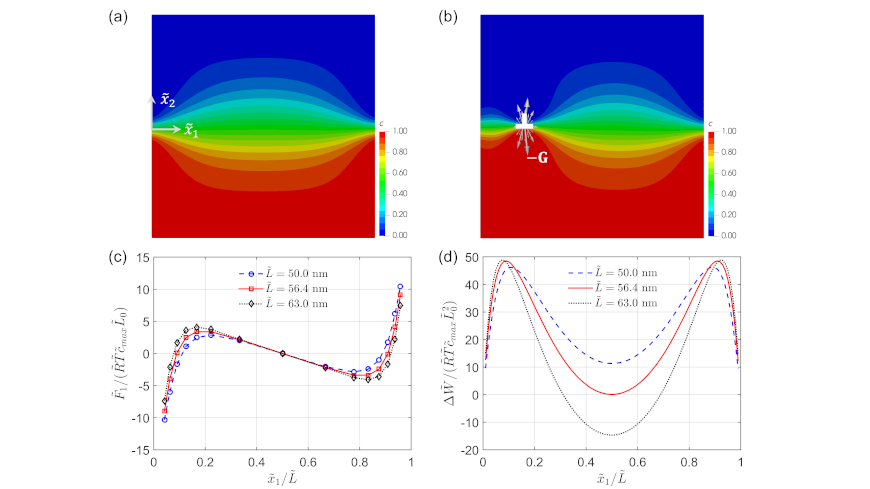
Dislocations in lithium-ion battery materials significantly influence the performance of the battery. A chemo-mechanical phase-field model combined with a non-singular continuum theory of dislocations is developed to simulate misfit dislocations at the phase boundary of two-phase LiFePO4 particles. The configurational mechanics of dislocations in the mechanically coupled phase transformation problem is proposed and then used to formulate a dislocation formation criterion. The model is numerically implemented using the finite element method to compute driving forces on misfit dislocations. The driving force is further used to study the stability of the misfit dislocation to predict the critical size of dislocation-free two-phase electrode particles. The orthotropic and non-homogeneous elastic constants in two phases, anisotropic misfit strain, different aspect ratios of the particle, and different positions of the phase boundary in equiaxed particles are considered. The large misfit strain at the phase boundary is found to cause a redistribution of the concentration and thus a relaxation of the stress field at the interface. Stress relaxation is crucial to the driving force on the dislocation and ignoring the stress relaxation leads to an underestimation of the critical particle size. The critical particle size decreases with increasing aspect ratios and shows a saturation after aspect ratios above 2. An optimum aspect ratio of the dislocation-free electrode particle is around 1.5 which features the highest specific surface area.



